This is another case of taking an analogy too far (the other one I can think of is assuming that the rubber sheet analogy indicates that there is some extra spatial dimension$^1$). In this case, I'm assuming you're talking about the "balloon" analogy - the universe is expanding, like a balloon, but since there's no center, all bits of matter are on the surface of the balloon. This naturally leads to the idea that if you travel in one direction, you'll eventually come back to where you started. This is, unfortunately, not true.
Scientists often talk about the shape of the universe - how it is curved on a local or global scale. There are three possible categories, depending on one parameter, $Omega$:
- Positive curvature $to$ $Omega>1$
- Zero curvature $to$ $Omega=1$
- Negative curvature $to$ $Omega<1$
This diagram gives a good visual of each curvature:
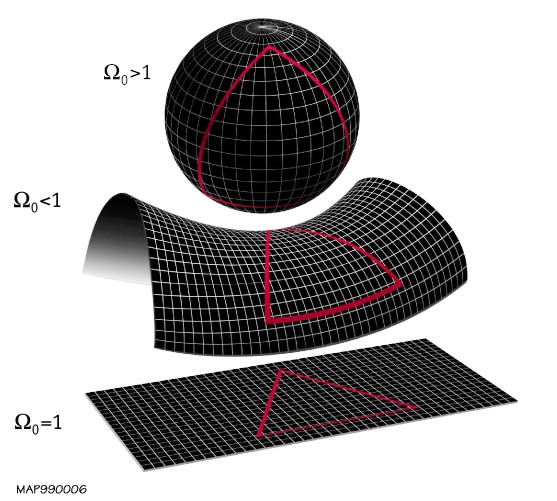
I should add that these are merely examples of universes (more accurately, manifolds) with each $Omega$. There are other cases with these curvatures, and so other universe where you can start at one point and end at the same point, as in a 3-torus.
All of these shapes could exist. However, in our universe, the global curvature is one where $Omega approx 1$ - a flat universe. The measurements that essentially clinch this are from the WMAP probe, which has analyzed the CMB and determined the age of the universe and its curvature. Measurements show, to a decent degree of accuracy, that our universe is flat - and so if we started in one direction, we would never return to where we started. Check out the NASA page for a full rundown of WMAP's results.
$^1$ Good questions dealing with this can be found here, here and here; John Rennie's answer on Physics is especially good.
No comments:
Post a Comment